Pour cette petite séance, je vous propose de vous expliquer simplement le principe de la projection. Ce principe peut être sympa à utiliser pour donner des effets de perspective à vos jeux vidéo !
La projection ? Kézaco ?
Le principe est assez simple. La projection permet de retranscrire dans un environnement 2D un ou plusieurs points 3D.
En d’autres termes, c’est le fait de transformer les coordonnées d’un point 3D x, y , z en coordonnées 2D x et y suivant le principe mathématique de la projection.
Maths obligatoires ?
Euh….non….enfin si 😀 Pas de panique ! c’est pas non plus horrible et facile à comprendre, de toute façon on va pas s’amuser à rentrer dans tous les détails, je ne suis pas mathématicien non plus hein ! Donc on se contentera d’utiliser des formules toutes faites.
Le principe
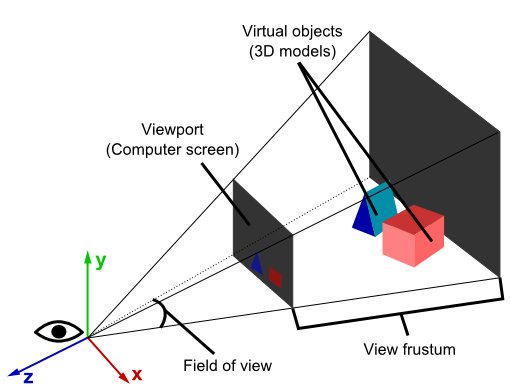
Le but est donc d’imaginer un objet 3D et de dire qu’on veut le projeter sur un écran 2D, quelles coordonnées cet objet aura t’il ? Cette question doit bien sur prendre en compte la position de l’objet dans le monde 3D, mais aussi l’orientation de l’écran et enfin la position de vos yeux qui regardent.
Avec tout ces paramètres on peut calculer les coordonnées 2D de chaque point 3D sur l’écran. Vu que ce n’est pas facile à expliquer, je vous montrer un schémas que j’ai trouvé sur un site qui résume bien ces propos :
C’est plus clair maintenant n’est ce pas ?
A quoi cela peut il bien servir pour le jeu vidéo ?
Grâce à une formule et à ce principe, il est possible de faire des effets sympathiques dans nos créations, pour simuler par exemple une perspective à l’écran. Si on regarde l’image du dessus, on pourrait remplacer l’écran cinéma par votre fenêtre de jeu Construct…Cela revient au même.
J’ai moi même illustré un peu ce principe dans une de mes créations (qui n’est pas un jeu) mais un semblant de moteur qui utilise justement la projection pour simuler un fond étoilé en perspective.
Vous pouvez essayer en html 5 ce moteur et télécharger le fichier source à cette adresse :
http://www.scirra.com/arcade/example/806/pseudo-3d-starfield
Comme vous pouvez le faire sur cette exemple, on croirait que le champs étoilé est en 3D, alors qu’il n’est rien, la position de chaque sprite est calculée suivant une projection. Bon j’avoue que dans cette exemple, j’ai un peu détourné la formule de base.
Mais l’important n’est pas d’appliquer à la lettre une formule, après vous pouvez « bidouiller » afin d’avoir l’effet souhaité.
La formule magique
Avant de vous donner la formule, nous allons considérer quelques points. En effet, cela ne sert à rien de lâcher une formule sans même comprendre ce qu’il y a dedans.
Comme on a l’habitude dans Construct de nommer nos objets, on va faire pareil ici. Nous avons besoin pour calculer tout cela, la position des yeux devant l’écran (coordonnées x , y , z), les coordonnées du point qu’on veut projeter à l’écran. C’est tout.
Généralement pour les coordonnées x et y des yeux du spectateur, on prend pour référence le centre. Donc dans un jeu si il est dans une résolution de 640 X 480 on prendra pour référence généralement le centre donc 320, 240. La coordonnée z pour les yeux, en revanche, est définie arbitrairement (comme on pourrait le faire avec la coordonnée z de l’objet à projeter).
Il faut bien comprendre que la coordonnée z représente la profondeur. Dans le cas de la position des yeux, il s’agit donc de la distance qui sépare nos yeux de l’écran.
Alors allons-y, nous allons appeler Yeux(x, y , z) pour désigner la position 3D des yeux qui regardent l’écran, Point(x, y , z), le point à projeter sur l’écran, Resultat(x, y ) les coordonnées 2D du point projeté, calculées grâce à la formule.
Pour trouver la coordonnée X du point projeté (donc Resultat.X) :
Yeux.z * (Point.x – Yeux.x)
Resultat.x = ————————————— + Yeux.x
Yeux.z + Point.z
La formule est simple au final. On multiplie la distance des yeux qui sépare l’écran (Yeux.z) par la différence entre la coordonnée x du points et la coordonnée x de la position des yeux. On divise le tout par l’addition de la distance qui sépare nos yeux de l’écran (Yeux.z) et la coordonnée z du point à projeter. Tout cela additionné à la coordonnée x de nos yeux.
Et hop vous avez la coordonnée projetée x du point sur l’écran.
Pour trouver la coordonnée Y du point projeté (donc Resultat.Y) :
Yeux.z * (Point.y – Yeux.y)
Resultat.y = ————————————– + Yeux.y
Yeux.z + Point.z
Comme vous pouvez le voir il n’y a aucune surprise, c’est exactement la même chose mais avec la coordonnée y.
Et voilà ! J’aurais très bien pu vous donner cette formule directe sans rien expliquer, mais cela n’aurait pas été d’une grande utilité !
Il est donc possible d’utiliser ce genre de formule dans vos créations pour faire créer des effets ! Bien entendu , je ne vous ai expliqué qu’une partie infime de la projection.
En effet, je ne suis pas mathématicien ou pro dans le domaine, et il y a des choses dans ce domaine qui sont bien plus compliquées. Cela dit j’espère qu’avec cet article vous aurez pu avoir une idée de ce qu’est la projection et à son utilité dans certaines situations.
A bientôt !